http://www.amherst.edu/~dacox/math23/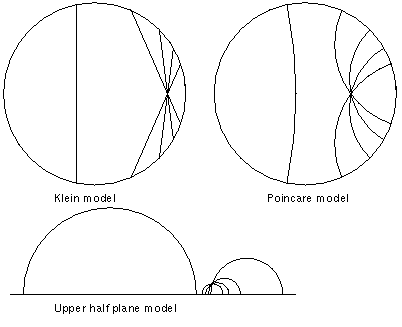
Math 23 Topics in Geometry
Fall 2001
Monday, Wednesday, Friday 1 pm
Seeley Mudd 205
David A. Cox
404 Seeley Mudd
Phone: 413-542-2082
Email: dac@cs.amherst.edu
Overview of the Course
The parallel axiom of Euclid asserts the existence of a unique
line through a given line and parallel to a given line. This axiom
is the foundation of much of the Euclidean geometry learned in
high school, including the Pythagorean Theorem and the fact that
the sum of the angles in a triangle sum to 180 degrees.
The "big idea" of Math 23 is to study what happens
when we no longer assume this axiom. For Fall 2001, the main topics
of Math 23 will be:
- Neutral Geometry, which is the study of what theorems in
geometry are valid with no assumptions about parallel
lines. We will see, for example, that one can prove that the
sum of the angles in a triangle is at most 180 degrees.
- Non-Euclidean Geometry, which is the geometry we get when
we assume the existence of more than one parallel line.
This wonderful geometry was discovered by Gauss, Bolyai, and
Lobachevski. In this geometry, the sum of the angles in a triangle
is strictly less than 180 degrees. Furthermore, this sum
determines the area of the triangle, so that there are no similar
triangles in Non-Euclidean geometry.
- Differential Geometry, which generalizes non-Euclidean geometry.
The central notion here is Gaussian curvature. A sphere
has constant positive curvature, and we will see that non-Euclidean
geometry has constant negative curvature. The latter will enable
us to construct some explicit models of non-Euclidean geometry.
One subsidiary topics we will explore is:
- General relativity, which asserts that gravity warps space
and makes it non-Euclidean. We will discuss Einstein's 1912 thought-experiment
which showed that the geometry of a rotating disk is not Euclidean!
Note: Our treatment of relativity will not assume any
previous knowledge of physics.
The figure shown above is from Models of the Hyperbolic
Plane by Evelyn Sander. Click here
for the full text of the article. Many interesting geometric images
can be found at the graphics
archive of the Geometry Center at the University of Minnesota.

